алгем теория
.pdf
Мнимый эллипсоид (#2)
Однополостный гиперболоид (#3)
Мнимая коническая поверхность (#6)
Эллиптический параболоид (#7)
Двуполостный гиперболоид (#4)
Гиперболический параболоид (#8)
Коническая поверхность (#5) |
Эллиптический цилиндр (#9) |
41
Мнимый эллиптический цилиндр (#10)
Гиперболический цилиндр (#11)
Пересекающиеся плоскости (#12)
Мнимые пересекающиеся плоскости
(#13)
Параболический цилиндр (#14)
42
Параллельные плоскости (#15)
Мнимые параллельные плоскости (#16)
Совпадающие плоскости (#17)
Уравнение сферы с центром в начале координат
Сфера является частным случаем эллипсоида, когда все его полуоси одинаковы (и равны радиусу сферы). Уравнение сферы с центром в начале координат и радиусом R выражается формулой
x2 + y2 + z2 = R2.
Уравнение сферы с центром в произвольной точке
(x − a)2 + (y − b)2 + (z − c)2 = R2,
где (a, b, c) − координаты центра сферы.
Уравнение сферы по заданным концам |
Общее уравнение сферы |
диаметра |
Ax2 + Ay2 + Az2 + Dx + Ey + Fz + M = 0, (A ≠ |
(x − x1)(x − x2) + (y − y1)(y − y2) + (z − z1)(z − |
0) |
z2) = 0, |
Центр сферы имеет координаты (a, b, c), |
где P1(x1, y1, z1), P2(x2, y2, z2) − конечные |
где |
точки диаметра. |
|
Уравнение сферы по четырем точкам |
|
|
Радиус сферы равен |
Точки P1(x1, y1, z1), P2(x2, y2, z2), P3(x3, y3, z3),
P4(x4, y4, z4) принадлежат данной сфере.
32. Линейные пространства.
Лине́йное простра́нство, или ве́кторное простра́нство, является обобщением понятия совокупности всех векторов n-мерного пространства. Линейные пространства — основной объект изучения линейной алгебры.
Пусть дано поле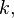 
элементы которого будем называть скалярами. Множество 
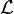называется
линейным или векторным пространством над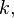 
а его элементы называются векторами, если на нём определены операции
векторного сложения |
обозначаемая |
где |
и |
умножения вектора на скаляр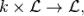 
обозначаемая 
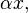где
удовлетворяющие следующим условиям:
1. |
|
2. |
|
3. |
где - мультипликативная единица в |
4. |
|
Простейшие свойства
1.Нейтральный элемент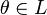 
является единственным.
2.
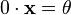для любого 
.
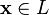3.Для любого 
противоположный элемент 
является единственным.
4.
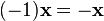для любого 
.
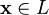5. |
для любых |
и |
. |
43
33. Собственные вектора линейных операторов
Ненулевой вектор 
называется собственным вектором линейного оператора
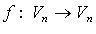, если 
(
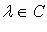для комплексного 
), такое, чт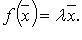о 
Число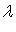 
называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.
Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор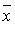 
имеет координатный столбец X, то 
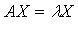или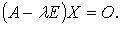 
Собственные числа 
линейного оператора 
- корни характеристического уравнения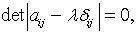 
, где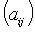 
- матрица оператора f, 
- символ Кронекера.
Для каждого собственного значения 
соответствующие собственные векторы могут быть
найдены из матричного уравнения 
или соответствующей ему системы линейных уравнений
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид
где 
- соответствующие собственные значения.
44
34. Квадратичные формы. Законоопределенность.
Квадратичной формой называется выражение S=a11x12+a22x22+a33x32+…+annxn2+2a12x1x2+2a13x1x3+…+
+2ann-1xnxn-1
Слагаемыми кв. формы являются квадраты переменных (x1,…,xn)
и их попарные произведения. |
В каждой кв. форме можно поставить матрицу кв. |
формы, которая будет иметь |
вид |
Матрица кв. формы представляет собой симметрическую матрицу, т.е. коэффициенты относительно главной диагонали равны. С помощью тождественных преобразований кв. форму можно привести к каноническому виду. В этом случае кв. форма будет иметь вид
S`=a11`x1`2+a22`x2`2+a33`x3`2+…+ann`xn`2
Законоопределенность квадратичной формы
1)Th: кв. форма называется знакоположительной, если все главные миноры являются положительными.
2)Th: кв. форма является знакоотрицательной, если знак главных миноров чередуется, начиная с отрицательного значения.
45