
Ответы к ГОСу / 5
.doc5. Пределы и непрерывность. Числовая последовательность и ее предел. Определение функции, ее непрерывность на языке "эпсилон-дельта" и языке пределов, равномерная непрерывность.
Если каждому значению n = 1,2,… ставится в соответствие по некоторому закону вещественное число xn, то множество занумерованных вещественных чисел x1, x2,…, xn,.. = {xn} называется числовой последовательностью. Это частный случай функции, аргумент которой принимает дискретные значеня.
Если даны 2 последовательности {xn} и {yn}, то последовательность {xn + yn} называется их суммой, {xn * yn} – произведением, {xn / yn} для yn 0 – частным.
Предел
Число A
называется пределом последовательности
при
![]()
![]()
 если
>0
такой номер N0>0:
n
> N0:
если
>0
такой номер N0>0:
n
> N0:
![]()
В любой окрестности точки A находятся все члены последовательности, начиная с некоторого номера.
Если существует
конечный
![]() ,
то последовательность называется
сходящейся.
В противном случае (если A
=
или lim
не )
последовательность называется
расходящейся.
,
то последовательность называется
сходящейся.
В противном случае (если A
=
или lim
не )
последовательность называется
расходящейся.
Точка x0 называется предельной точкой множества M, если в окрестности x0 содержится бесконечное множество точек множества M.
Если последовательность
имеет несколько предельных точек, то
значение самой большой предельной точки
называется верхним пределом
последовательности
![]() ,
а значение самой меньшей предельной
точки называется нижним пределом
последовательности
,
а значение самой меньшей предельной
точки называется нижним пределом
последовательности
![]() .
.
|
Пример. 1, 1-1/2, -1, 2, 1, 1-1/4, -2, 3, 1-1/8, -3, … n, 1-1/2n, -n, … Последовательность имеет 3 предельные точки +; 1; -
Последовательность расходящаяся. Последовательность может быть сходящейся, только если она имеет единственную точку (число). |
Последовательность
называется ограниченной,
если
M>0,
что для
![]()
Т: Из всякой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Т: Если последовательность сходится, то она является ограниченной. Обратное неверно.
|
Пример.
-1, 1, -1, 1, …, (-1)n
– ограничена, т.к.
Но не сходится, так как 2 предельные точки |
Если
![]() ,
то последовательность {xn}
называется бесконечно малой.
,
то последовательность {xn}
называется бесконечно малой.
Если
![]() – бесконечно большой.
– бесконечно большой.
|
Связь неограниченная
Неограниченный: для M > 0 n0N: |xn| M Бесконечно большая: для >0 N0: для всех n>N0: |xn| > n = N0+1 |xn| > M n бесконечно большая неограниченная. Обратное не верно: |
|
|
|
xn=n*sin n неограниченная не бесконечно большая
|
Функция
Функцией y = f(x) называется закон, по которому каждому значению xD(f)R ставится в соответствие единственное действительное число yR.
При этом множество значений аргумента D(f) называется областью определения функции, а множество значений {y | y = f(x), xD(f)} называется множеством значений функции.
Функция может быть задана аналитически (то есть формулой), таблично или графически.
y=x2
![]()
Если функция задана таблично, то чтобы найти значение функции для промежуточных значений аргумента применяют интерполяцию, заменяя функцию линейной, квадратичной на участке между двумя значениями аргумента.
Пусть точка x0 является предельной точкой области определения функции, тогда
![]() для
> 0
> 0:
xD(f)
O(x0)
\ {x0}:
f(x)
O(A)
для
> 0
> 0:
xD(f)
O(x0)
\ {x0}:
f(x)
O(A)
(O – -окрестность).
|
Зачем \ {xn}. Например
f(x0=0) = 3 O(1) |
Левосторонний предел
![]() для
> 0
> 0:
x:
для
> 0
> 0:
x:
![]()
![]()
Правосторонний предел
![]() для
> 0
> 0:
x:
для
> 0
> 0:
x:
![]()
![]()
Двусторонний предел
![]()
![]()
![]()
Непрерывность
Функция f(x) называется непрерывной в точке x0, если:
-
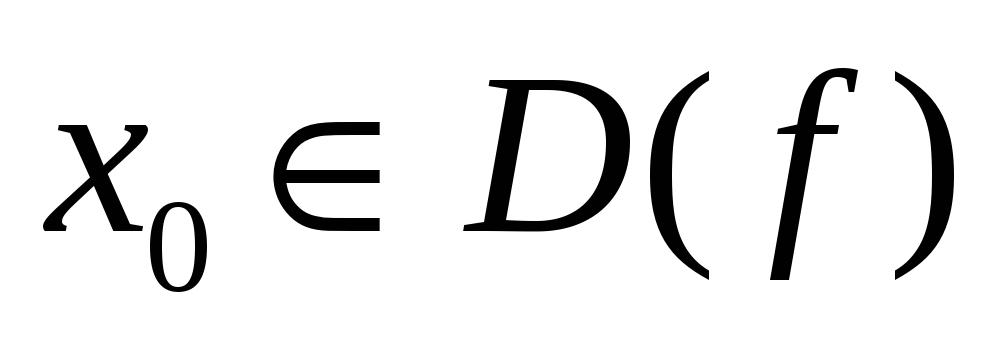
-
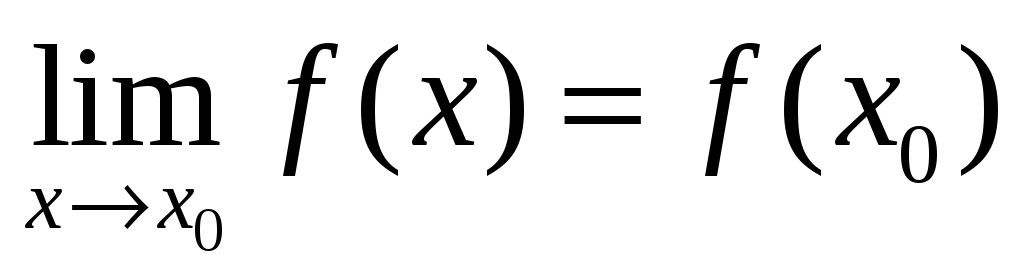 .
.
На языке пределов: функция f(x) называется непрерывной в точке x0, если она:
1) определена в этой точке;
2)
![]()
На языке ε и δ: функция f(x) называется непрерывной в точке x0, если:
1)
![]()
2) для > 0 > 0: x: | x – x0| < δ: | f(x) – f(x0)| < ε.
|
1. Если x0 является предельной точкой D(f)
f f(x0–) = B <
x0 – разрыв I рода, скачок |
2 пределов = или не , то x0 – точка разрыва II рода
|
Разрыв называется
устранимым, если существуют
![]() и конечны. (Пример: y
= x2
/ |x|)
и конечны. (Пример: y
= x2
/ |x|)
Если функция непрерывна в каждой точке множества X, то она непрерывна на множестве X.
Сумма
![]() ,
произведение
,
произведение
![]() ,
частное
,
частное![]() ,
суперпозиция
,
суперпозиция
![]() есть функция непрерывная.
есть функция непрерывная.
Все элементарные функции непрерывны в своей области определения
x, ax, logax, sin x, cos x, tg x, ctg x, arcsin x, arcos x, arctg x, arcctg x – основные элементарные функции.
Элементарные функции из основных элементарных получаются с помощью конечного числа операций сложения, деления, умножения, суперпозиции.
|
Исследовать на непрерывность, точки разрыва
Функция элементарна. В своей области определения непрерывна
0 – предельная
точка для ОДЗ. Но функция не определена
в 0
|
Пример
|
Определение непрерывности функции по Гейне
Функция непрерывна в точке x0, если:
1. она определена
в точке x0,
то есть
![]() ;
;
2. для ![]() последовательность
последовательность
![]() .
.
|
Функция Дирихле определена, но разрывна во всех точках
|
Т1. Если f(x) определена в некоторой окрестности точки x0 и непрерывна в точке x0 и f(x0)>0, то такая окружность O(x0) точки x0: f(x) > 0
Теорема Больцано-Коши [о нуле]. Если функция f(x) непрерывна на сегменте [a, b], выполняется f(a)*f(b) < 0
тогда с[a, b] f(c)=0
Теорема Больцано-Коши [о промежуточном значении]. Пусть функция f(x) непрерывна на [a;b], f(a) = , f(b) = , – между и , тогда с[a, b]: f(с) =
Теорема Вейерштрасса 1. Если функция непрерывна на сегменте [a, b], то она ограничена на нем.
Теорема Вейерштрасса 2. Если функция непрерывна на [a, b], то она достигает на нем своих наибольшего и наименьшего значений.
Теорема Кантора. Если функция непрерывна на [a, b], то она равномерно непрерывна на [a, b].
Функция y = f(x) называется равномерно непрерывной на множестве М, если > 0 > 0: x1, x2 M из |x1 – x2|< δ => |f(x1)-f(x2)|< ε. Всякая равномерно непрерывная функция является непрерывной в каждой точке множества М. Обратное неверно. Если функция непрерывна на множестве М, то для данного ε нужное δ может быть своим для каждой т.x1. В случае равномерной непрерывности для заданного ε δ, обслуживающее все множество М.

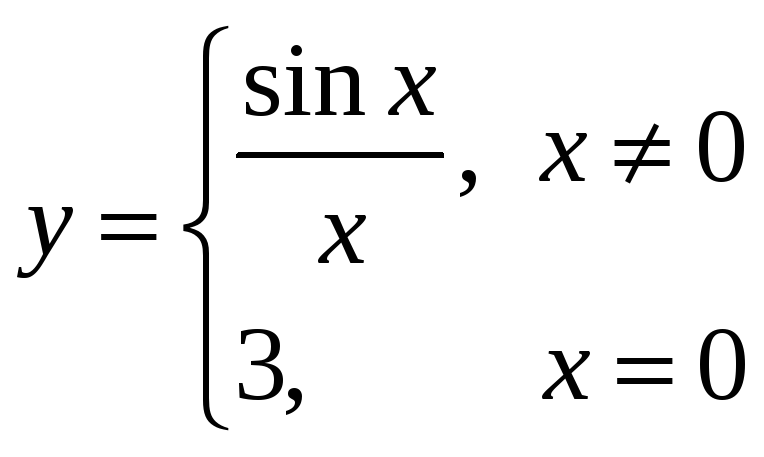
 (x0+)
=
A
<
(x0+)
=
A
<  .
Если хотя бы один из односторонних
.
Если хотя бы один из односторонних