
glava01
.pdf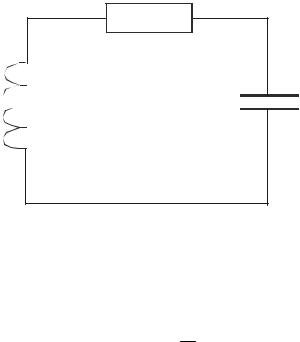
R

 L C
L C
Рис. 1.4. Электрический контур с потерями
К примеру, уравнение, описывающее процессы в линейном колебательном контуре (рис 1.4):
L d 2q + R dq + 1 q = 0. dt2 dt C
Обозначив 2δ = R / L , 1/ LC =ω02 ; q = x, приходим к уравнению (1.25).
Очевидно, что параметр 2δ характеризует потери в рассматриваемой системе. Для колебательного контура это потери энергии, обусловленные нагреванием сопротивления R, в механических системах – это потери, обусловленные трением. Вышеперечисленные случаи соответствуют системам с так называемым положительным трением (δ > 0).
Между тем существует большое число примеров, когда энергия поступает к осциллятору извне, приводя на линейной стадии процесса к раскачке колебаний. Примером таких систем являются автоколебательные, преобразующие энергию от постоянного источника в энергию колебательного процесса.
Уравнение, описывающее процессы в автоколебательной системе на начальной стадии, как будет показано ниже, формально совпадает с (1.25), но параметр δ отрицателен. Подобные системы называют осцилляторами с отрицательным трением.
Таким образом, параметр δ характеризует трение – положительное или отрицательное. Параметр же ω02 в общем случае, как видно из рассмотрения консервативной системы, характеризует возвращающую ( ω02 > 0) либо отталкивающую ( ω02 < 0) силу [4].
При анализе гармонических осцилляторов, описываемых уравнением (1.25), рассматривают следующие случаи.
19
1.В системе действует возвращающая сила и есть небольшое поглощение или отрицательное трение, ω02 > 0, ω02 > δ2.
2.В системе действует возвращающая сила и есть большое положительное или отрицательное трение, ω02 > 0, ω02 < δ2.
3.B системе действует отталкивающая сила, ω02 < 0.
Рассмотрим фазовый портрет колебаний для каждого из этих случаев. Общее решение (1.25) имеет вид
|
|
|
x = Aeλ1t + Beλ2t , |
(1.26) |
||
где λ1,2 = −δ ± |
δ2 − ω02 − корни характеристического уравнения, |
соот- |
||||
ветствующего (1.25). |
|
|
|
|
|
|
При ω2 > δ2 |
λ |
− комплексно-сопряженные величины: |
|
|||
0 |
1,2 |
|
|
|
|
|
|
|
λ |
= −δ ± jω , ω = ω2 −δ2 .. |
|
||
|
|
1,2 |
1 |
1 |
0 |
|
Тогда |
|
|
|
|
|
|
|
|
|
x = De−δt cos(ω t +ϕ), |
(1.27) |
||
|
|
|
|
|
1 |
|
A = 12 De− jϕ , B = 12 De jϕ.
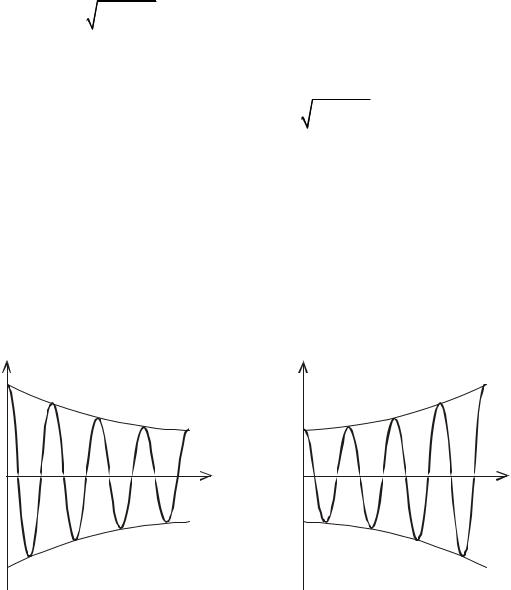
Зависимость координаты x от времени показана на рис 1.5.
Видно, что движения осциллятора больше не являются периодическими, поэтому понятия периода и частоты колебаний теряют смысл.
x |
a |
|
δ > 0 |
||
|
||
|
t |
x |
б |
|
δ < 0 |
|
t |
Рис. 1.5. Графики движения в системах с положительным (а) и отрицательным (б) трением
20

Тем не менее здесь сохраняются некоторые черты периодического процесса: положение равновесия осциллятор проходит за равные интервалы времени Т/ 2, T = 2π/ ω, а максимумы и минимумы следуют с периодом T.
Всвязи с этим параметры Т и ω называют соответственно периодом
ичастотой затухающих колебаний.
Можно показать, что за период Т амплитуда уменьшится в e−d раз,
где d = δT − логарифмический декремент затухания. Затухание в осцил-
ляторе характеризует и другой, более употребляемый параметр – доб-
ротность:
Q = dπ = 2ωδ .
Добротность − это число периодов Т, за которое амплитуда колеба-
ний уменьшается в eπ раз.
Для получения уравнения фазовых траекторий подстановкой приведем (1.25) к виду
dy |
|
2 |
x |
. |
|
||
|
|
= −2δ − ω |
|
|
|||
dx |
y |
|
|||||
|
0 |
|
|
||||
Введя z = y/x, получим |
|
|
|
|
|
|
|
dx |
= − |
zdz |
|
|
. |
||
x |
z2 + 2δz + ω02 |
||||||
|
|
|
|||||
y = dx dt
dt
(1.28)
Если провести интегрирование (1.28) с учетом того, что ω02 > δ2 , то получим
2δarctg |
y+δx |
|
||
ω1x . |
||||
y2 + 2xyδ+ω2 x2 = c2eω1 |
|
|||
0 |
|
|
|
|
Введя новые переменные u = y +δx, v = ω1x, |
придем к уравнению |
|||
2δarctg u |
||||
u2 +v2 = c2eω1 |
ν |
|||
или, перейдя к полярным координатам u =ρsin θ, ν =ρcosθ, |
||||
2δθ |
(1.29) |
|||
ρ2 = c2eω1 . |
||||
Уравнение (1.29) описывает семейство логарифмических спиралей на плоскости u, v. Переход от координат u, v к координатам z, y приведет к
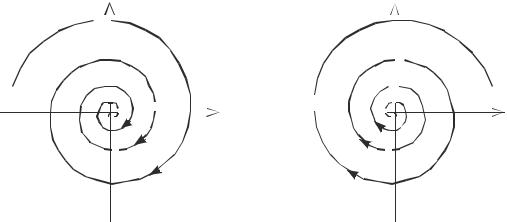
деформации спиралей. Качественный вид фазовых траекторий показан на рис. 1.6.
21
а |
y |
|
|
|
|
б |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
δ > 0 |
δ < 0 |
Рис. 1.6. Фазовые траектории в системах с положительным (а) и отрицательным (б) трением
Положение равновесия осциллятора с затуханием (δ > 0) соответствует на фазовой плоскости особой точке типа устойчивый фокус (рис. 1.6, а). Все траектории со временем стремятся в эту точку, асимптотически приближаясь к ней при θ→ −∞. Устойчивый фокус является простейшим примером аттрактора. Аттрактором динамической системы называется множество в фазовом пространстве, к которому стремятся все достаточно близкие к нему траектории.
Аттракторов в динамической системе может быть много (в том числе и бесконечно много). Они определяют характер режима, который устанавливается в системе после переходного процесса.
Если в системе действует отрицательное трение, δ < 0, то логарифмические спирали раскручиваются от фокуса (рис. 1.6, б). В этом случае фокус неустойчив. Колебания в системе происходят с возрастающей амплитудой (см. рис. 1.5, а).
Итак, в рассмотренном случае слабого затухания, δ2 < ω02 , движение осциллятора сохраняет черты колебательного процесса.
Исследуем случай сильного затухания δ2 > ω02 при наличии возвращающей силы ( ω02 > 0 ).
Общий вид решения исходного уравнения (1.25) тот же, что и в предыдущем случае. Однако λ1,2 − вещественны и, следовательно, (1.26) опи-
сывает неколебательные лимитационные движения. Для нахождения фазовых траекторий в этом случае воспользуемся более простым методом.
Выпишем значения x и y:
x = Aeλ1t + Beλ2 t ,
y = dxdt = Aλ1eλ1t + Bλ2eλ2 t .
22

Первое уравнение умножаем сначала на λ1, затем на λ2. Вычитая из второго первое, получаем два уравнения:
y − λ1x = B(λ2 − λ1 )eλ2 t ,
y− λ2 x = A(λ1 − λ2 )eλ1t .
Врезультате их объединения нетрудно прийти к соотношению
λ2
(y −λ x)= c( y −λ |
2 |
x) λ1 . |
|
(1.30) |
||
1 |
|
|
|
|
|
|
Как видно из (1.26), при ω2 |
> 0 |
отношение λ |
2 |
/ λ > 0 , так как кор- |
||
0 |
|
|
|
|
1 |
|
ни характеристического уравнения будут иметь одинаковые знаки: при δ > 0, λ1 < 0, λ2 < 0, при δ < 0, λ1 > 0, λ2 > 0. Следовательно, уравнение
(1.30) описывает семейство парабол. В зависимости от начальных условий получаются также уравнения прямых, проходящих через начало координат y = λ1x, y = λ2 x . Все кривые и прямые имеют общую точку в
начале координат. Эта особая точка называется узлом. Для случая положительного трения узел – точка устойчивого равновесия (устойчивый узел), для отрицательного трения – узел неустойчивый. Качественный вид фазовых траекторий показан на рис 1.7.
Сравнительно легко также проанализировать зависимость x(t) на основании (1.26). При положительном трении ( λ1 и λ2 отрицательны) уравне-
ние может иметь положительный корень x(t) = 0. Значит, система один
раз проходит положение равновесия в некоторый момент времени, затем достигает максимума, а затем стремится к нулю (рис. 1.8, кривая 1). Если
a |
y |
|
|
|
δ > 0 |
|
x |
б |
y |
|
|
|
δ < 0 |
|
x |
Рис. 1.7. Фазовый портрет системы с сильным затуханием
23

x |
3 |
2 |
t |
1 |
Рис. 1.8. Возможные варианты движения |
в системе с сильным затуханием |
же корень (1.26) отрицателен или корней нет, то возможны два случая: либо осциллятор монотонно стремится к положению равновесия (рис. 1.8, кривая 2), либо сначала достигает какого-то максимума отклонения, а затем возвращается к положению равновесия (рис. 1.8, кривая 3).
Построение фазовых траекторий для случая отталкивающей силы легко провести, используя предыдущие результаты. Уравнение фазовых траекто-
рий имеет вид (1.30). Однако при ω2 < 0 |
λ |
2 |
/ λ < 0, так как корни λ |
и λ |
2 |
|
0 |
|
1 |
1 |
|
||
имеют разные знаки при δ > 0 и δ < 0. |
Значит, соотношение (1.30) в этом |
|||||
случае описывает семейство гипербол с асимптотами y = λ1x, |
y = λ2 x, про- |
|||||
ходящими через особую точку – седло. Седло, независимо от знака трения, – неустойчивая особая точка. Вид фазовых траекторий показан на рис. 1.9.
y |
x |
Рис. 1.9. Фазовый портрет системы с отталкивающей силой |
24

Отметим, что уравнение осциллятора с отрицательным трением не может описывать систему на бесконечном интервале времени. Со временем значение x(t) станет настолько большим, что будут нарушены сделанные при выводе уравнения предположения и для описания динамики реальной системы необходимо использовать более общую нелинейную модель.
1.5.ОБЩАЯ КЛАССИФИКАЦИЯ ОСОБЫХ ТОЧЕК НА ФАЗОВОЙ ПЛОСКОСТИ
Исследованными в предыдущих параграфах случаями ограничиваются все «типичные» виды особых точек не только для линейного ДУ (1.25), но и для произвольной нелинейной системы. Это обусловлено тем, что для нелинейных систем исследование характера фазовых траекторий вблизи особых точек базируется на линейном приближении.
Введя систему координат δ, ω02 , можно отобразить на плоскости пара-
метровδ, ω02 области, вкоторыхреализуютсяразличныетипыособыхточек.
Показанные на рис. 1.10 особые точки являются типичными: при произвольно выбранных параметрах динамической системы ее положения равновесия будут характеризоваться какими-то особыми точками. Если
предположить, что параметры δ и ω02 зависят от некоторой величины p, характеризующей систему, то точка, отвечающая текущим значениям δ(p) и ω02 ( p), будет двигаться вдоль определенной линии. Пока точка нахо-
дится внутри одной из областей, показанных на рис. 1.10, небольшое изменение параметра не меняет типа особой точки и характера траекторий
|
δ |
|
Устойчивый узел |
|
|
|
|||
|
|
|
||
|
|
|
δ2= ω2 |
|
|
|
|
0 |
|
|
|
|
C |
|
Седло |
|
|
Устойчивый фокус |
|
|
|
B |
|
|
|
|
|
||
|
|
|
ω2 |
|
|
|
|
0 |
|
|
|
|
A Неустойчивый фокус |
|
|
|
|
Неустойчивый узел |
|
|
|
|
|
|
Рис. 1.10. Области реализации различных типов особых точек
25

вблизи нее. Если же значения δ и ω02 таковы, что точка находится на од-
ной из границ (точки A, B, C на рис. 1.10), то малое изменение параметра приводит к изменению типа особой точки и вида фазовых траекторий. Такое перестроение фазового портрета системы называется бифуркацией, а значение параметра, при котором оно происходит, – бифуркационным.
Пример бифуркации – превращение устойчивого фокуса линейного осциллятора при δ < ω0 в устойчивый узел δ > ω0. Бифуркационным значением является δ = ω0.
В математике и физике существует понятие грубости или структурной устойчивости. Суть этого понятия в том, что при малом изменении параметра грубая система хоть и изменяет в деталях режим функционирования, но не принципиально. С этой точки зрения для грубых систем переход через точку бифуркации означает смену одного структурно устойчивого режима на другой. В частности, в точке бифуркации δ = ω0 система не является грубой: малое изменение параметра в ту или иную сторону приводит к резким изменениям состояния.
Различают мягкие и жесткие бифуркации. Для пояснения рассмотрим два простых примера. В первом случае (см. рис. 1.11) в результате бифуркации исходное стационарное состояние теряет устойчивость и рождаются два новых устойчивых стационарных состояния. При этом вновь появившиеся два стационарных состояния (рис. 1.11, в) расположены в непосредственной близости от исходного состояния, которое потеряло устойчивость (помечено звездочкой). Бифуркации такого типа называют мягкими, имея в виду то, что вновь родившийся режим функционирования системы как появляется из режима, потерявшего устойчивость, и осуществляет рядом с ним.
Рис. 1.11. Пример мягкой бифуркации. Стационарное состояние (a) теряет устойчивость (б) и вблизи него появляются два новых стационарных состояния (в)
Другой пример бифуркации качественно представлен на рис. 1.12. При определенных значениях параметров, характеризующих систему (рис. 1.12, а) шарик находится в устойчивом состоянии. При этом суще-
26

ствует еще одно, неустойчивое состояние (помечено звездочкой). В точке бифуркации устойчивое и неустойчивое состояния сливаются в одно (рис. 1.12, б). Далее они исчезают и система выбирает новый режим (например, как это показано на рис. 1.12, в), который существенно отличается от предыдущего и не находится в непосредственной близости от исходного режима. Такой тип бифуркаций называют жестким. Жесткие бифуркации являются предметом анализа в теории катастроф.
Рис.1.12. Жесткая потеря устойчивости стационарным состоянием, катастрофа.
В результате безусловно упрощенного, качественного описания проблемы устойчивости и бифуркаций динамических систем можно, тем не менее, сделать определенные выводы. Эволюция любых систем сопровождается потерей устойчивости одними режимами функционирования и бифуркационными переходами их в новые. Эти “фазовые переходы” могут осуществляться плавно, мягко, а могут происходить скачкообразно, в виде катастроф. Строгий анализ устойчивости и бифуркаций позволяет рассматривать широкий спектр проблем, связанных с исследованиями бифуркационных переходов в различных динамических системах. Но при этом необходимо опираться на строгие математические результаты и использовать обоснованные методы теоретического и качественного анализа.
27

1.6.КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
СОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
ПОД ДЕЙСТВИЕМ ВЫНУЖДАЮЩЕЙ СИЛЫ
Как уже отмечалось, свойства колебаний в системе под действием внешней периодической силы – так называемых вынужденных колебаний, зависят не только от параметров системы, но и от амплитуды, частоты и фазы внешней силы. Различают два вида внешнего воздействия – силовое и параметрическое. При силовом воздействии, которое будет рассмотрено в данном параграфе, параметры системы не изменяются. Параметрическое же воздействие на систему осуществляют изменением во времени энергоемких параметров системы.
Четкая классификация колебательных систем по признаку внешнего воздействия (параметрическое или силовое) возможна только для линейных систем. Если система нелинейна и на нее действует внешняя сила, то нелинейные параметры системы будут изменяться во времени. Вследствие этого в колебательной системе будут возникать явления, характерные для обоих видов внешнего воздействия.
Итак, исследуем поведение линейного гармонического осциллятора под действием внешней периодической силы. Примеры осциллятора показаны на рис. 1.13.
а |
б |
|
|
|
|
R
E(t) L
F(t) |
C |
|
Рис. 1.13. Примеры осцилляторов, находящихся
под действием внешней периодической силы
Очевидно, что эталонное уравнение, описывающее поведение линейного осциллятора, имеет вид
d 2 x + 2δdx +ω2 x = F(t). |
(1.31) |
||
dt2 |
dt |
0 |
|
|
|
||
28
