Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Vetrov_Sunchalina_Timonin_Teor_ver (fn1)

.pdf

Скачиваний:

Добавлен:

09.02.2015

Размер:

467.05 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Найдем вероятность попадания в интервал(0,5;1,5).

(

0,5;1,5

))

(

)

− F(0,5) = e−0,5625 −e−0,0625

≈ 0,37.

F 1,5

При

подсчете числовых характеристик

случайной

величины ξ

удобно использовать

∞

гамма-функцию Эйлера Γ(α)= ∫tα−1e−tdt

, обладающую свойствами:

Γ(α +1)=α Γ(α),

Γ(1)=1,

π .

Найдем математическое ожидание

ξ .

∞

−

∞

Μ(ξ)= ∫ x f (x)dx =∫

dx =∫

−t

2t2 e dt = 2Γ

= 2

= π .

−∞

Здесь

интеграле использована

замена переменной

t = x4 / 4.

Аналогично находим

дисперсию ξ .

∞

(x − Μ(ξ))2

∞

D (ξ)

= ∫

f (x)dx = ∫ x2 f (x)dx −(Μ(ξ))2 =

−∞

∞

e−

∞

= ∫

dx −π =∫4te−tdt −π = 4Γ(2)−π = 4Γ(1)−π = 4 −π.

Среднеквадратическое отклонение

σ (ξ)=

≈ 0,93.

D (ξ)

4 −π

Пример 9. Плотность распределения вероятностей

случайной величины ξ имеет

вид

fξ (x) =

kx,

x [0;1,5]

Случайная величинаη

связана

с ξ функциональной

x [0;1,5]

зависимостью

η = 4ξ2 −7

Найти: 1)

константу

k ;

математическое ожидание и

дисперсию случайной величины η , используя плотность распределения вероятностей

случайной величины ξ ; 3)функцию распределения и	плотность	распределения
вероятностей случайной величины η и построить их	графики; 4)	математическое

ожидание и дисперсию случайной величины η , используя найденную плотность распределения вероятностей.

				∞
Решение. Константу k находим из условия нормировки ∫ fξ (x)dx =1. Получаем
				−∞
∞	1,5	9k		8 .
∫	fξ (x)dx = ∫kxdx =	9k	=1. Следовательно k =	8 .
−∞	0	8		9

Для вычисления математического ожидания случайной величины η воспользуемся формулой Μ(η)= Μ(g (ξ ))= ∞∫ g (x)fξ (x)d . Получаем

										−∞
			1,5									8					8					7				1,5		5
			1,5																							1,5
Μ(η)= ∫(4x							2	−7)						xdx		=				4	−		x	2			= −		.
Μ(η)= ∫(4x								−7)				9		xdx		=	9		x		−	2	x				= −	2	.
Дисперсия			0																							0
			0																							0

D (η)= D (g (ξ ))= ∞∫ g2 (x)fξ (x)dx −(Μ(η))2 =																											1,5∫(4x2 −7)2			8 xdx −	25	=
						−∞																					0			9	4
=	8	16	x	6	−	56			x	4	+		49		x	2		1,5		25		=	27		.
	8	16		6		56				4			49			2		1,5		25			27
																			−
	9	6					4							2				0			4		4
	9	6					4							2				0			4		4

Найдем функцию распределения случайной величиныξ .

x < 0

8 t dt,

4 x2 ,

)

∫

(

t dt =

0 ≤ x ≤1,5

ξ (

)

∫

−∞

x >1,5

Далее ищем функцию распределения случайной величины η .

x < −7

x +7

Fη (x)= Ρ(η < x)= Ρ(4ξ

−7 < x)= Ρ

−

< x <

, −7 ≤ x ≤ 2 =

x > 2

x < −7

x +7

= Fξ

− Fξ

−

, −7 ≤ x ≤ 2

−0,

−7 ≤ x ≤ 2 =

x > 2

x < −7

(x +7),

−7 ≤ x ≤ 2

x > 2

По определению плотности распределения случайной величины

1 , x [−7;2] fη (x)= Fη′(x)= 9

0, x [−7;2]

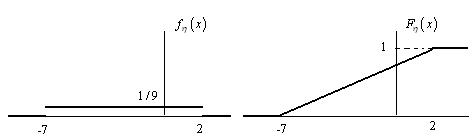
Таким образом, случайная величина η имеет равномерное распределение на отрезке

[−7;2]. Графики ее плотности и функции распределения изображены на рисунке 7.

Найдем числовые характеристики случайной величины η , используя ее плотность распределения. Для математического ожидания получаем

Μ(η)= ∞∫	x fη (x)dx =∫2	x	1 dx =		x2	2	= −	5 .


−∞	−7		9	18		−7		2

Рис. 7. Плотность и функция распределения случайной величины η Аналогично, находим дисперсию случайной величины η .

D(η)= ∞∫	x2 fη (x)dx −(Μ(η))2 =∫2	x2 1 dx −	25	=	x3	2	−	25	=	27 .

			4					4
−∞	−7	9		27		−7				4

Видим, что результаты подсчета числовых характеристик различными способами совпадают.

Пример 10. Дана система двух дискретных случайных величин (ξ,η), закон

xi \ yj	-1	0	2		4	распределения которой задан таблицей. Найти: 1)
						законы распределения случайных величин								ξ и η ;			2)
1	0,1	0	0,15		0,05	законы распределения случайных величин								ξ и η ;			2)
1	0,1	0	0,15		0,05
						математические ожидания					и дисперсии			случайных
3	0,15	0,15	0		0,1	математические ожидания					и дисперсии			случайных
3	0,15	0,15	0		0,1
						величин ξ		и	η ; 3) коэффициент корреляции							rξη ;	4)
5	0,2	0	0,1		0	величин ξ		и	η ; 3) коэффициент корреляции							rξη ;	4)
						условные		распределения			Pξ (xi	y3 ),	Pη (yj		x3 );		5)


условные математические ожидания Μ(ξ							y3 ),		Μ(η	x3 ).
условные математические ожидания Μ(ξ							y3 ),		Μ(η	x3 ).
Решение.		Найдем		законы		распределения			случайных		величин ξ		и	η .		Пусть
pij = Ρ(ξ = xi ,η = yj ),				i =1,2,3		y =1,2,3,4 .Тогда

piξ = Ρ(ξ = xi )= ∑pij ,	pηj = Ρ(η = yj )= ∑pij . Простые вычисления дают законы
j	i

распределения случайных величин ξ и η ( их удобно изображать на таблице совместного распределения, добавив один столбец справа и одну стоку снизу).

xi	1	3	5

piξ	0,3	0,4	0,3

yj	-1	0	2	4
pηj	0,45	0,15	0,25	0,15

Ищем числовые характеристики случайных величин.

Μ(ξ)= ∑xi piξ =1 0,3 +3 0,4 +5 0,3 = 3;

Μ(η)= ∑yj pηj = (−1) 0,45 +0 0,15 +2 0,25 +4 0,15 = 0,65;

D (ξ)= ∑xi2 piξ −(Μ(ξ))2 =1 0,3 +9 0,4 +25 0,3 −9 = 2,4;

D (η)= ∑y2j pηj −(Μ(η))2 =1 0,45 +0 0,15 +4 0,25 +16 0,15 −0,4225 =1,9775.

Для подсчета коэффициента корреляции случайных величин ξ и η сначала найдем их ковариацию.

cov (ξ,η)= Μ(ξη)−Μ(ξ)Μ(η)= ∑∑xi yj

pij −Μ(ξ)Μ(η)=1 (−1) 0,1+1 2 0,15 +

i j

+1 4 0,05 +3 (−1) 0,15 +3 4 0,1+5 (−1) 0,2 +5 2 0,1−3 0,65 = 0,7.

Коэффициент корреляции

ρ(ξ,η)=

cov(ξ,η)

0,7

≈ 0, 23.

D (ξ)D (η)

2, 4 1,9775

Далее находим условные законы распределения по формулам

Pξ (xi

y3 )

Pη (yj

x3 )=

p3 j

-1

Pξ (xi

y3 )

0,6

0,4

Pη (yj

x3 )

2/3

1/3

Пример 11. Дана система двух непрерывных случайных величин (ξ,η) с совместной

C, (x, y) D		. Область	D	ограничена кривыми
плотностью распределения f (x, y)=	0, (x, y) D

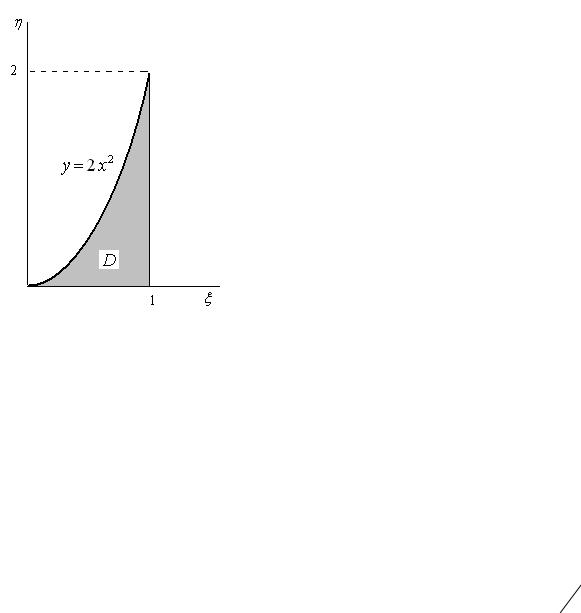
x =1, y = 0, y =2 x2 . Область D показана на рисунке 8.

Рис. 8. Область D , на которой задано распределение (ξ,η)

Найти: 1) совместную плотность распределения

f (x, y) , предварительно построив

область

D ; 2) плотности вероятности случайных величин ξ

и η ; 3) математические

ожидания и дисперсии случайных величин ξ

и η ;

4) коэффициент корреляции rξη ; 5)

условные плотности распределения

fξ (x

fη (y

x);

условные математические

ожидания Μ(ξ

y),Μ(η

x), уравнения линий регрессии и построить их графики.

Решение.

Константа

определяется

из

условия

нормировки

1 = ∫∫ f (x, y)dx dy =∫1 dx

C dy =C ∫1

2∫x

2 x2 dx =

2C x3 │10

2С .

Отсюда С = 3

Ω

Область D уже показана на рисунке 8.

Плотность fξ (x)

случайной величины

определяется

интегрированием

совместной плотности

f (x, y)

по

всем возможным

при данном

ξ = x

значениям

случайной величины η (из рисунка непосредственно видно, что

0<η<2 x2 ). Имеем

∞∫

fξ (x) =

f (x, y)dy =

2∫x

3 dy =3x2

, 0

< x <1. Совершенно аналогично

fη (y) =

−∞

∫1

3 dx =

−

), 0 < y < 2.

3. Математические ожидания и дисперсии каждой величины ξ, η определяются согласно формулам для вычисления моментов скалярных случайных величин (см., например, пример 9). Имеем

							∞									2																			y2																2
			Μ(η)												3							y								3									2									5			2				3		8			3
															3							y								3									2									5							3		8			3
						= ∫ y fη				( y) dy =						∫y			1−					dy =								(					−									y			2 )		=					(2 −			) =		.
						= ∫ y fη				( y) dy =					2	∫y			1−		2			dy =						2		(	2				−									y			2 )		=				2	(2 −	5		) =	5	.
							−∞								2	0					2									2			2					5 2													0				2		5			5
							−∞									0										1												5 2													0
			Μ(ξ )= ∞∫ x fξ (x) dx =∫1 x 3x2dx = (																			3x4 )						=			3 .
			Μ(ξ )= ∞∫ x fξ (x) dx =∫1 x 3x2dx = (																			3x4 )						=			3 .
							−∞						0										4			0					4
D (η)= ∞∫ y2 fη (y)dy −(Μ(η))2 =																				∫2 y2 (1−																											y3											2
																		3								y			)dy							9					3			(									2			y7 2 )		2		9		37	.
																		3								y								−		9			=		3									−			2					−		9	=	37
																		2							2											25					2

			−∞																	0																									3						7				2			0	25		175
			−∞																	0																				1											7				2			0
D (ξ)= ∞∫ x2 fξ (x)dx −(Μ(ξ))2 =∫1 x2 3x2dx −																												9			=				(3x5				)			−				9				=		3		.
																												9																		9						3
																											16																		16						80
			−∞													0											16									5				0					16						80
			−∞													0																rξη								0
4.					Коэффициент											корреляции																rξη										вычисляется																	по			формуле
rξη =	M (ξη				)−M (ξ) M (η)										.	В этом выражении неизвестен только смешанный момент
rξη =															.	В этом выражении неизвестен только смешанный момент
					D(ξ) D(η)
второго порядка M (ξ η) .
																														2													∫1 2x5 dx =
	M (ξη)=∫∫x y f (x, y)dx dy =																				3	∫1 x dx2∫x										y dy = 3											∫1 2x5 dx =													1
							D														2	0								0									2				0													2
								1 −			3		3
Тогда r							=	2			4		5	≈0,56.
Тогда r							=							≈0,56.
					ξη				3				37
									3				37
									80			175
									80			175
5. Условные плотности распределения																												fξ (x							y) и						fη (y								x)определяются по формулам
5. Условные плотности распределения																												fξ (x							y) и						fη (y								x)определяются по формулам
fξ (x		y)=		f (x, y)					=				32							=			1					. Необходимо обратить внимание на то, что
				f (x, y)									32										1

					f		(y)			3							y				1−				y
					f		(y)																		y
					η								1−
																									2
																2
												2				2

возможные значения аргумента x здесь зависят от y и меняются в пределах

,1 .

Переменная

y здесь играет

роль

параметра

и может

принимать

любое

значение

промежутке

[0,2]. Рассуждая

аналогично,

получим

для

fη (y

выражение

fη (y

x)=

f (x, y)

; 0 < y < 2x2;0 < x <1.

fξ (x) 3x2

2x2

(

)

(

)

6. Общие формулы для условных математических ожиданий

Μ η

имеют вид Μ(ξ	y)= ∞∫ x fξ (x / y)dx,	Μ(η	x)= ∞∫ y fη (y / x)dy . Учитывая замечание


	−∞		−∞

предыдущего пункта о возможных значениях случайной величины при фиксированном значении другой случайной величины, получим

																														2
																												y
																									1			y							y
1																		2		1							−	2					1+
1																		2		1							−
Μ(ξ	y)= ∫ x			1			dx =				1						x							=								=		2		.
				1							1						x																	2

					y								y			2													y					2
	y		1−		y			1	−				y			2					y					2(1−			y		)			2
		2	1−	2				1	−					2					2							2(1−		2			)
		2		2										2														2
	2x2		1			1			y	2		2x2				4x		4
	2x2									2		2x2						4
Μ(η	x)= ∫																					2
																						2
		y	2x2	dy =		2x2			2						=	4x2				=x			; .
			2x2			2x2			2							4x2
0												0
0												0

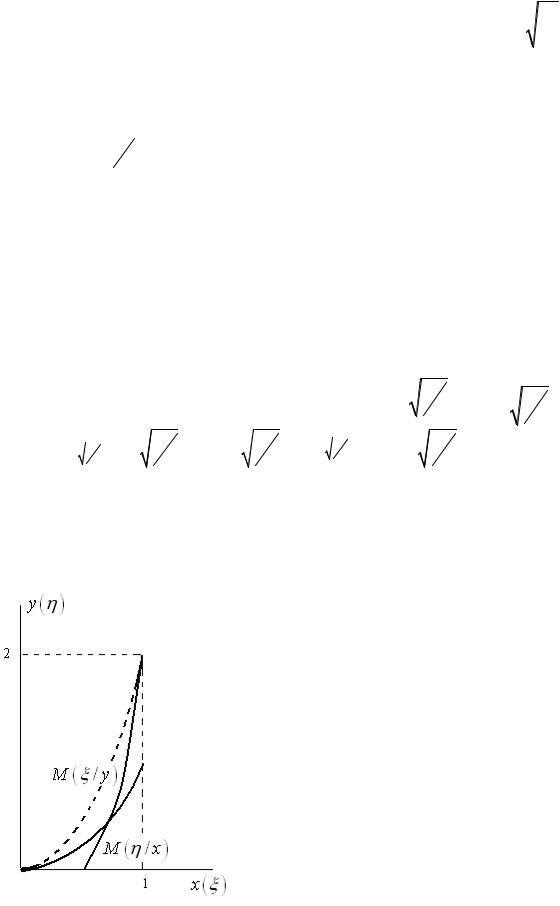
Графики условных математических ожиданий показаны на рисунке 9.

Рис.9. Графики условных математических ожиданий

Пример 12.

а)

Найти

математическое

ожидание

дисперсию

случайной

величины

z =3ξ −8η + 4, где (ξ,η) - система случайных величин из примера 11;

в) Найти функцию распределения, плотность и математическое ожидание площади

прямоугольника с вершинами в точках (0,0), (0,η), (ξ ,0),

(ξ,η ), где (ξ,η)

- система

случайных величин из примера 11.

Решение.

а)

M (z) = M (3ξ −8η + 4) =3Mξ −8Mη + 4 =

9 −

+ 4 =

D(z) = D(3ξ −8η + 4) = D(3ξ −8η)=9Dξ + 64Dη + 2 3 (−8) cov(ξ,η) =

=9Dξ + 64Dη + 2 3 (−8) (M (ξη) − Mξ Mη) = 27 +

2368 − 48

≈

≈11,49.

175

в) Так как ξ > 0, η > 0,

то площадь прямоугольника

равна

S =ξ η. Проще

всего вычислить среднее значение MS = M (ξη) = cov(ξ,η) + Mξ Mη = 0,5 .

Нетрудно видеть, что возможные значения

лежат в интервале [0,2]. Функция

распределения FS (z)случайной величины S

вычисляется как интеграл от совместной

плотности

f (x, y)

по области

Dz ={(x, y)

x y < z D, 0 < z < 2}

(см. рисунок 10).

Разбивая

область

интегрирования

на

две

частиD = D1

D2 ,

{

}

{

}

D1 =

(x, y)

x y < z D, 0 < x

< x

, D2

(x, y)

x y < z D, x

< x <1

где

= 3

- абсцисса точки пересечения кривых y = 2x2 ,

x y = z , получим

FS (z) =P(ξ η < z) = ∫∫ f (x, y)dx dy = ∫∫ f (x, y)dx dy + ∫∫ f (x, y)dx dy =

2x2

dy + 3

z x

0x0 +

3 z ln x

1x0

∫dx

∫

∫dx ∫dy =

∫2x2 dx +

∫

dx =x3

2 x

1−ln(

) , 0 < z ≤2 .

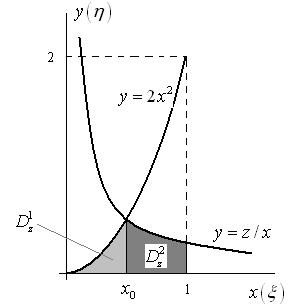
								1	ln	2
Тогда плотность f	S	(z) имеет вид	f	S	(z) = F	′(z) =		2	ln	z	, z (0,2 .
	S			S	S			2		z
									z (0,2]
							0,		z (0,2]

Рис. 10. Разбиение области интегрирования

2. Задачи типового расчета.

Задача 1. Одновременно подбрасывают две игральные кости. В вариантах 1-10 найти вероятность того, что сумма выпавших очков: 1) равна k ; 2) меньше k +1; 3) больше k −1; 4) заключена в промежутке [α;β]. В вариантах 11-30 найти вероятность

того, что произведение выпавших очков: 1) равно k ; 2) меньше k +1; 3) больше k −1; 4) заключено в промежутке [α;β].

Задача 2. На некоторое обслуживающие устройство поступают две заявки. Каждая мо жет по ступить в любо й мо мент вр емени в т ечение Т минут. Время обслуживания первой заявки τ1 минут, второй - τ2 минут. При поступлении заявки на занятое устройство

она не принимается. При поступлении заявки			на свободное устройство даже в последний
момент времени Т , она		обслуживается. Найти вероятность того, что: 1) обе заявки будут
обслужены; 2) будет обслужена ровно одна заявка.
Задача 3. Задана		структурная схема	надежности системы, состоящей	из пяти
элементов. Событие		- отказ i -го элемента за некоторый промежуток		времени.
	Аi

Вероятности безотказной работы элементов заданы:

P(Ai ) = 0,95,	i =1,3,5;	P( Aj ) = 0,9,	j = 2,4.
Событие А	состоит в	безотказной	работе всей системы за рассматриваемый

промежуток времени (события Аi независимы в совокупности). Требуется: 1) выразить событие А через Ai или Аi ( i =1,2,3,4,5); 2) найти вероятность P(А) безотказной работы системы.

Задача 4. Из партии, содержащей n изделий, среди которых k - высшего сорта, для контроля последовательно выбирают наугад m изделий. Найти вероятность того, что среди выбранных изделий окажется ровно высшего сорта при условии, что выборка производится: 1) с возвращением (выбранное изделие после проверки возвращается обратно в партию); 2) без возвращения (выбранное изделие в партию не возвращается).

Задача 5. На склад поступили детали, изготовляемые на трех станках. На i -м станке изготовлено Ri % деталей (i =1,2,3). Вероятность выпуска бракованных деталей на i -м станке равна Pi (i =1,2,3) . 1) Определить вероятность того, что деталь, наудачу взятая со склада оказалась бракованной. 2) Наудачу взятая деталь оказалась бракованной. Найти вероятность того, что она изготовлена на j-м станке.

Задача 6. В отдел технического контроля поступает партия, содержащая N изделий, среди которых имеется M бракованных. Контролер для контроля отбирает 3 изделия, при этом в бракованном изделии он обнаруживает брак с вероятностью P . Партия бракуется, если среди трех отобранных для проверки изделий обнаружено хотя бы одно бракованное изделие. Найти вероятность того, что данная партия изделий будут забракована.

Задача 7. Произведено n независимых выстрелов по мишени с вероятностью попадания p . Пусть случайная величина ξ - число попаданий в цель. Для случайной величиныξ найти: 1) распределение вероятностей; 2) функцию распределения и построить ее график; 3) вероятность попадания случайной величины в интервал (α;β); 4)

математическое ожидание, дисперсию и среднеквадратическое отклонение.


Задача 8. Непрерывная случайная величина ξ		имеет плотность распределения
вероятностей	f (x) . Для случайной величины ξ найти : 1)		ее функцию распределения
F(x) и построить графики функции распределения		F(x)	и плотности распределения
вероятностей	f (x) ; 2) вероятность попадания случайной величины в интервал (α;β); 4)

математическое ожидание, дисперсию и среднеквадратическое отклонение.

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.11.2018559.1 Кб30Ver_5_ОснЗаконы.doc
#
05.11.2018574.98 Кб26Ver_6_Системы2.doc
#
05.11.2018645.63 Кб46Ver_7_Норм2.doc
#
05.11.2018448.51 Кб32Ver_8_СистемыN.doc
#
05.11.2018806.91 Кб24Ver_9_ЧХ_Функции_СВ.doc
#
09.02.2015467.05 Кб47Vetrov_Sunchalina_Timonin_Teor_ver (fn1).pdf
#
10.02.2015215.84 Кб38VHDL lection.pdf
#
10.02.2015730.19 Кб153VHDL.pdf
#
09.02.20157.31 Mб296Visual Basic 2005 (word97).doc
#
21.09.2019261.37 Кб3Vitalina_variant_11.docx
#
07.05.2019154.11 Кб8Vlasko_N_K_Introduction_to_Control_SAU_6_sem.doc